Polyominoes

A polyonmino is the name given to plane figures created by groups of squares touching at their edges. Polyominoes are generally referred to in groups, sharing a characteristic number of sides, ignoring rotations and reflections. For example, the monomino is the trival group consisting of a single square. Nearly everyone is familiar with the shape of the domino, a rectangle consisting of two side-by-side squares. The trominoes are slightly more interesting: this group has two members, referred to as the "straight tromino" and the "right (angle) tromino".

Polyominoes made of four squares are referred to as tetrominoes, and there are five of these. The popular arcade puzzle game "Tetris" challenges players to interlock these polyominoes while leaving as few holes as possible.


The five-square polyominoes are called the pentominoes. Twelve distinct pentominoes exist. For convenience, each can be thought as resembling a letter of the alphabet and hence is given a "letter name".



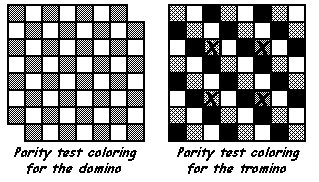
An interesting mathematical problem is given a set of n squares, how many n-ominoes are there? We shall denote this number by P(n). As of 1994, P(n) has been calculated for values of n up to n=24; D. H. Redelmeier calculated that P(24) = 654,999,700,403. It is believed (though not proven) that P(n+1)/P(n) will continue to increase as n increases.

n
1
2
3
4
5
6
7
8
9
10
11
12
P(n)
1
1
2
5
12
35
108
369
1285
4655
17073
63600


A series of interesting problems concerns covering all the squares of an 8-by-8 checkerboard. For monominoes and dominoes this is obviously possible. Less obvious is whether a checkerboard with opposite corners removed can be covered by dominoes. This is proven false by a "parity test": the squares of the checkboard are colored as in the diagram, and it is noted that each domino will cover one light and one dark square. Since the number of dark and light sqaures are unequal, this board cannot be covered by dominoes. A similar parity test can be used to show that right trominoes can cover the checkerboard with one square removed, provided it is one of the squares marked with an "X" in the diagram. The checkboard (with no squares removed) can be covered by any of the tetrominoes except the skew one. Additionally, it is possible to cover the checkerboard using one of each of the twelve pentominoes plus a square tetromino.



The pentominoes seem to lend themselves to the greatest number of intriguing puzzles, probably because the number of pentominoes is small enough to be easily managed yet large enough to be combined and arranged in a multitude of ways.
Click here for a large set of pentominoes that you can print and cut out.


An easy set of puzzles with the pentominoes consists of using them to form rectangles of dimensions 3 by 20, 4 by 15, 5 by 12, and 6 by 10.

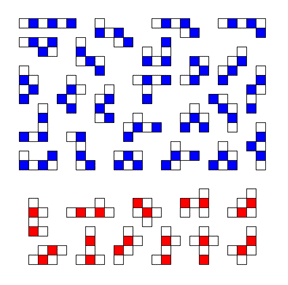Another set of pentomino puzzles is found in the triplication problem: Given a pentomino, use nine other distinct pentominoes to construct a scale model three times as long and as wide as the given pentomino. An example of a triplication of the X pentomino is shown to the right.


To the left are the 35 hexominoes.


And here is a quick look into the realms of higher polyominoes:

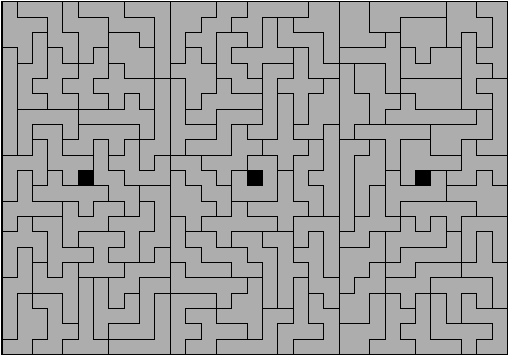
First, here are all of the heptominoes packed into a rectangle, with three symmetrical holes.



And here are all the octominoes, packed into a rectangle. The holes in the packing are unavoidable because six octominoes contain an unreachable square unit.



I would like to post a picture of the 9-ominoes in a rectangle. If such a construction or picture exists (or does not exist), please send me an email... you will be credited! Thanks!

Return to Mathematrix