Mobius Strip
Look at a normal sheet of paper. Count the number of sides. There's two - a front and a
back, right? Pretty typical.
Here's how you make a not-so-typical piece of paper.
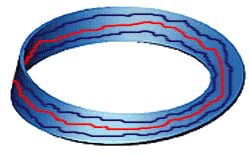
Take a long, thin strip of paper... 4 cm by 24 cm, for example. Anything reasonably close
will do. Give one end a half twist and then tape it together. It should look
similar to this:
(except it doesn't have to be blue.)

What you now have is a one-sided, one-edged piece of paper called the Mobius strip. To see
that it has only one side, try drawing a line along one side and continue until you end up
where you started. Like this:
Now see if you can find the "other side"... the side without a line on
it. You won't find the other side, because there isn't one!

To see that there is only one edge, use a different colored pencil or pen and draw a line
along the edge on one side of the center line you drew.
Eventually you will end up where you started, and you will see
that there are lines along "both" edges of the Mobius strip.
But since you drew only one continuous line, there must be only one edge!
Now think about what would happen if you cut down the center of your Mobius strip. An
ordinary paper ring cut in half would give you two seperate rings, right? However, if
you cut down the center of a Mobius strip, instead you end up one ring twice as large as
the original!
For another (different) unexpected result, try cutting the strip one-third of the distance
from the edge. I won't discuss what happens here... from experience I have found that it is
more enjoyable to be suprised. So have fun!
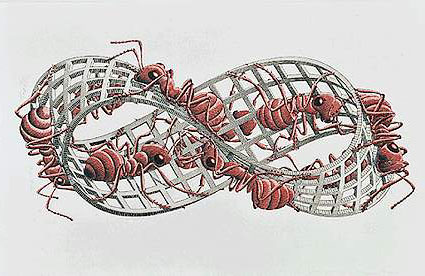
One last amusement... the ants below are walking on a
Mobius strip. So even though one ant may be above or below another, they are still on the
same side!
Return to Mathematrix
Take a long, thin strip of paper... 4 cm by 24 cm, for example. Anything reasonably close
will do. Give one end a half twist and then tape it together. It should look
similar to this:
(except it doesn't have to be blue.)
(except it doesn't have to be blue.)

What you now have is a one-sided, one-edged piece of paper called the Mobius strip. To see
that it has only one side, try drawing a line along one side and continue until you end up
where you started. Like this:
Now see if you can find the "other side"... the side without a line on
it. You won't find the other side, because there isn't one!
Now see if you can find the "other side"... the side without a line on it. You won't find the other side, because there isn't one!

To see that there is only one edge, use a different colored pencil or pen and draw a line
along the edge on one side of the center line you drew.
Eventually you will end up where you started, and you will see
that there are lines along "both" edges of the Mobius strip.
But since you drew only one continuous line, there must be only one edge!
But since you drew only one continuous line, there must be only one edge!

One last amusement... the ants below are walking on a Mobius strip. So even though one ant may be above or below another, they are still on the same side!
