Flexagons
In 1939 a Princeton graduate student, Arthur Stone, played around with a strip of
paper trimmed from his notebook and created the first flexagon. A flexagon is a polygon,
usually made from paper, that can be folded in certain ways to produce a series of faces.
If that description didn't make any sense, you have two options: visit the homepage of David
King and look at his very excellent
Java Flexagon Animation . Otherwise you can continue reading and it should all make
sense after constructing one yourself.
There are many different varieties of flexagons. The specific name of each flexagon has two
prefixes, the first
stating how many faces can be made to appear, and the second giving the shape of the
flexagon. For example, a trihexaflexagon is in the shape of a hexagon and it has three
different faces that may come up while folding; a hexatetraflexagon is shaped like a square
or rectangle and has six different faces. That's all there is to it.
On this page you will find instructions on folding four different types of hexaflexagons.
In addition, David King has generously let me use his instructions, which I have colored
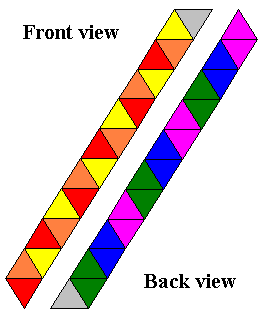
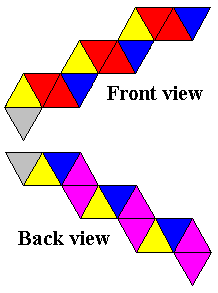
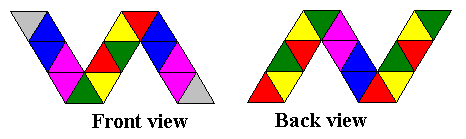
for your convenience. Triangles that are the same color end up on the same face when the
flexagon has been constructed (with the exception of the gray faces, which are the two ends
glued or taped together in the last step of each construction). Also provided for your benefit
are .gif files (thanks again to David King!) that may be printed and cut out, saving you the trouble of trying to draw
all those triangles yourself.
General instructions for the diagrams
How to flex (fold) your flexagon
Diagrams
Trihexaflexagon ---- printable model
Tetrahexaflexagon ---- printable model
Pentahexaflexagon ---- printable model
Hexahexaflexagon ---- printable model
Tuckerman traversals
David King's Flexagon Page
(includes flexagon theory articles. excellent page!)
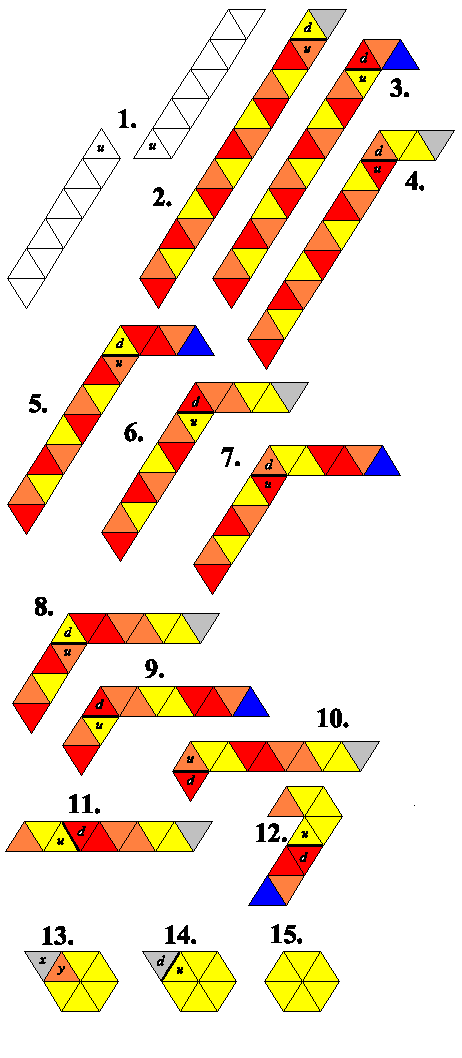
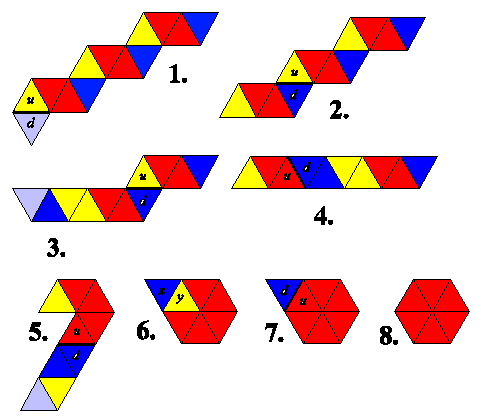
General instructions
First of all, fold along every crease line on the strip, back and forth,
ready for easy flexing.
For convenience, you may wish to number the sides according to color.
Now start at step 1. and go through each step in order. Each step
(except for the third-to-last) has a heavy line with 2 faces marked u and d.
Fold along the heavy line, so that after the fold u faces up and d faces down onto the
table.
In one diagram, there is a triangle underneath y. Tuck the mini strip x and y
beneath this, so you can only see x.
In the second to last diagram, stick the two faces u and d together with glue or double sided tape.
How to flex (fold) your flexagon
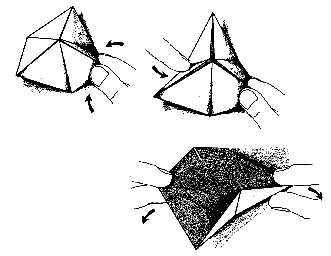
First, pinch together two triangles at a corner of the hexagon. Push the opposite corner down
and in towards the center. You can now open out the middle to reveal a new face.
If you can't get it to work, try the next corner.
Tuckerman traversal
This term refers to the following diagram that shows the different sequences in which faces
may appear while flexing a hexahexaflexagon. Each circle contains two different colors which
correspond to the sides of one possible orientation of the hexaflexagon. All the different
orientations possible by a single flex are those circles connected by lines.

Trihexaflexagon
printable model
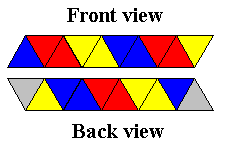

Tetrahexaflexagon
printable model
Pentahexaflexagon
printable model

Hexahexaflexagon
printable model