Higher Dimensions
Before we start talking about higher dimensions, let's briefly review the lower ones:
0th dimension: a point.
It has no length, width, or breadth.
1st dimension: a line segment.
It has a length.
It is created from moving a point.
2nd dimension: a square.
It has length and width.
It is created from moving the line segment
in a direction perpendicular to the line on
which the segment lies.
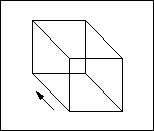
3rd dimension: a cube.
It has length, width, and depth.
It is created from moving the square in
a direction perpendicular to the plane.
And for some reason, it seems to stop there. Or does it? Granted we do not see the
four-dimensional analog of the cube (referred to as a hypercube or a tesseract) in our
space, but does that mean it doesn't exist? Although I'm sure none of you have seen one,
I bet you can describe its properties. Look at the following table:
Shape
Points
Edges or Line segments
Faces or Squares
Solids or Cubes
Tesseracts
Point
1
n/a
n/a
n/a
n/a
Line Segment
2
1
n/a
n/a
n/a
Square
4
4
1
n/a
n/a
Cube
8
12
6
1
n/a
Tesseract
?
?
?
?
?
Well, it should be apparent that the number of points doubles every time you increase a
dimension. So a tessact has 16 points. Next, think about how the square traces out
a cube as it is moved perpendicular to the plane. The cube's edges (or lines) come from the initial
four lines of the square while it is in the plane, the four lines of the sqaure once it has
been moved to its final position, and the four points on the square as they move through space. In much the same manner, the tesseract
gets 12 of its edges from the initial position of the cube, 12 more edges from the final position,
and the eight points of the cube trace out 8 more edges at the cube moves in a direction
perpendicular to three-dimensional space. This is a total of 32 edges. By similar
deduction, you should find that the tesseract also contains 24 square faces and 8
solids (the concept of a "solid" face is difficult to imagine, seeing as how our
senses are inadequate to percieve it.)
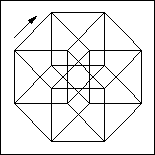
4th dimension: a tesseract.
It has length, width, and depth, and a
fourth "length" we will call hyperlength.
It is created from moving the cube in
a direction perpendicular to regular three-dimensional space.
That's all I will say on the subject for now... the best way to come to an understanding of higher dimensions is by analogy: how would a two-dimensional creature visualize three-dimensional space? The best exposition of this process is in Flatland, written by
Edwin A. Abbott. I have posted the entire book (it's really rather short) online. Including
pictures! Click here for the text. You really should read it.
It's also a great story!
Return to Mathematrix
0th dimension: a point.
It has no length, width, or breadth.
1st dimension: a line segment.
It has a length.
It is created from moving a point.
2nd dimension: a square.
It has length and width.
It is created from moving the line segment
in a direction perpendicular to the line on
which the segment lies.
3rd dimension: a cube.
It has length, width, and depth.
It is created from moving the square in
a direction perpendicular to the plane.
Shape
Points
Edges or Line segments
Faces or Squares
Solids or Cubes
Tesseracts
Point
1
n/a
n/a
n/a
n/a
Line Segment
2
1
n/a
n/a
n/a
Square
4
4
1
n/a
n/a
Cube
8
12
6
1
n/a
Tesseract
?
?
?
?
?
4th dimension: a tesseract.
It has length, width, and depth, and a
fourth "length" we will call hyperlength.
It is created from moving the cube in
a direction perpendicular to regular three-dimensional space.