The Euler Society Newsletter

Volume 1, number 1
January, 2002

Visit the Euler Society home page at
http://www.eulersociety.org

Join The Euler Society

Use the membership form at The Euler Society's home page. $50 per year.

Call for Papers

The Euler Society calls for papers to be presented at the E2K+2 Conference, August 4-7, 2002 (See below). The Call for Papers is on line at http://www.euler2007.com/CallForPapers_1.htm or you can contact the Editor at esandifer@earthlink.net and he will send you a copy.

Euler and Andrew Wiles?

Did Andrew Wiles follow in Euler’s footsteps when he worked in secret on one of his era’s great unsolved problems? We all know the story of Andrew Wiles and his seven years in the attic working in secret on Fermat’s Last Theorem. Did Euler work in secret on the Basel Problem, his first great mathematical breakthrough? In one of his early papers, E-20 (O.O. I.14 25-41), written in 1730/31, Euler gives a six decimal place approximation of the value of Zeta(2). Other than that, though, he doesn’t seem to mention the Basel Problem either in his papers or his correspondence until he publishes the complete solution in E-41, "De summis serierum reciprocarum", written in 1734/35 and published in 1740. (O.O. I.14 73-86).

At the Bookstore

Here we review books and other resources on Euler that should be still available in bookstores and on line. Please send ideas for book reviews to the editor at esandifer@earthlink.net.

Euler The Master of Us All

MAA

In the Treasure Room

We describe books and other resources on Euler that are out of print, or may even be called "antiquarian," so that readers might know what to look for in libraries and used book stores and what they might be getting if they buy or bid on line. Please send ideas for book reviews to the editor at esandifer@earthlink.net.

Leonhard Euler

Opera Omnia

Price cut for the Opera Omnia?

Ten years ago, Birkhäuser, the publishers of Euler’s Opera Omnia, sold volumes of Series I for about $65. About the time they were bought by Springer Verlag, the prices soared to the range of $190 to $220, and it was very difficult to get them delivered in North America. Now, with the advent of the Euro, Birkhäuser’s web site offers them for E 150 (150 Euros, about $135). We optimistically await reports of improved service.

Call for limericks

Continuing a vile tradition in newsletters of Certain Societies on the History or Philosophy of Mathematics, we shamefacedly solicit limericks, clerihews, haiku and other short poetry related to the life, works and influence of Leonhard Euler. Send them to the Editor at esandifer@earthlink.net.

Call for contributions

The Newsletter will gladly include short contributions about Euler, his life, works and influence, and we will provide links to longer contributions. Contact the Editor at esandifer@earthlink.net.

Euler in San Diego

Historians of Mathematics enjoyed some lively sessions at the Joint Mathematics Meetings in San Diego in early January. Of course, Euler was a popular topic. Here are short descriptions of some of the talks about Euler.

"Euler and Cevians" – Homer White, Georgetown College
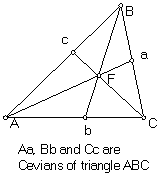
A really nice talk about one of Euler’s late papers, E-749 (O.O. I.26 344-358) about when the sides of a triangle can be translated to make cevians of a new triangle. For our readers who are not Geometers, the figure at the right illustrates what cevians are. They are three line segments, each joining a vertex of a triangle with a point on the opposite side, with the special property that the three segments intersect in a single point. Segments Aa, Bb and Cc are cevians because they all pass through the point F. In this paper, Euler admits to "longae ambagae", or "extensive wanderings."
"The Quadrature of Lunes, from Hippocrates to Euler" – Stacy Langton, University of San Diego
Euler followed up on Hippocrates’ work with papers in 1737 (E-73 O.O. I.26 1-14) and 1771 (I’m not sure what paper this is), showing that there really aren’t very many lunes for which Hippocrates’ construction works.
"The crescents of Hippocrates from the second millennium BCE to the second millennium CE" – Una Bray, Skidmore College
Una added to the remarks Stacy Langton had made the day before, and showed how some lunes are almost constructible.
"Euler and the Greatest Homework Ever" – Ed Sandifer, Western Connecticut State University.
An account of how Euler did the first general work on Calculus of Variations as a homework assignment for his mentor in Basel, Johann Bernoulli. The homework was published and is E-9 (O.O. I.25 1-12)
"Priority, Propriety and Polemic: The Euler-d'Alembert Correspondence" – Robert Bradley, Adelphi University
Rob told us how Euler and d'Alembert got along for a while, then didn't, and compared how their lives were so similar in some ways, so different in others.

HOMSIGMAA

The MAA has a new Special Interest Group, HOMSIGMAA (History of Mathematics Special Interest Group of the Mathematical Association of America), which came into being as the result of hard work by Rob Bradley and Amy Shell. HOMSIGMAA doesn't yet have a page at the MAA Web site. For now, it's hosted by Rob Bradley here.

Upcoming Math History events

February 6, 2002, Bill Dunham at the Pohle Colloquium, Adelphi U. Garden City, NY. It's not Euler, but it's Bill Dunham.
April 15, 2002, Leonhard Euler's 295^th birthday
May 24-26, 2002, CSHPM annual meeting - Toronto
August 1-3, 2002, MathFest in Burlington, Vermont
August 4-7, 2002, E2K+2, Rumford, Maine. See below.

Euler 2K+2

The Euler Society's first big event is scheduled for Rumford, Maine, August 4-7, 2002, hot on the heels of the MathFest in Burlington. You can register on line at http://www.euler2007.com.

On This Date in Euler's Life

We use Old Style dates for events in Russia, New Style elsewhere.

January 7, 1751 Euler reads E-245, (O.O. I.22) "De methodo Diophantaneae analoga in analysi infinitorum" in Berlin.
January 14, 1751 Euler reads E-250 (O.O. I.25 98-122)"Sur le probleme isoperimetrique" to the Berlin Academy.
January 18, 1748 Euler reads E-148 (O.O. I.26 46-59), "Sur le nombre des points oú deux lignes des orders quelconques peuvent se couper" before the Berlin Academy.
February 1, 1748 Euler reads E-149, (O.O. III.2 )"Réflexions sur l'Espece et sur le Tems" before the Berlin Academy.
February 6, 1766 Bernoulli reads Euler's last two Berlin papers, one on Lunar theory (E-401 O.O. II.26) and one on optics (E-360 O.O. III.7)
February 23, 1747 Euler reads E-100 (O.O. I.2 59-61), On Amicable Numbers, before the Berlin Academy, and increases the number of known pairs of amicable numbers from 3 to 30.
February 27, 1773 Euler's last letter from d'Alembert