Platonic Solids
The Platonic Solids are five very special polyhedra.
Consider a plane. It is flat and two dimensional. It is easy enough to construct polygons,
i.e.
Triangles, Quadrilaterals, Pentagons, and so forth. Furthermore, we may require that all
their sides and angles are equal. We call such a figure a regular polygon. And it
should be pretty obvious that one can construct a regular polygon with any number of sides
that we want. So we say there are an infinite number of different regular polygons.
Now say we wanted to construct an analogous figure in three dimensions - a regular
polyhedron. For a polyhedron to be regular, it should have the same regular polygon
as each of its sides, and each vertex (corner) should have the same number of polygons
around it. One may think at first that one can construct an infinite number of regular
polyhedra in three-dimensions, just as we could construct an infinite number of regular
polygons in two-dimensions. However, this does not turn out to be the case. In fact,
there are only five regular polyhedra! They are called the platonic solids.
With a bit of thought, one can see that no more than five regular polyhedrons. A corner of
a polyhedron must have at least three faces, the simplest of which is an equilateral
triangle. We can form a vertex by putting together three, four, or five equilateral
triangles. If we use more than five, the angles total 360 degrees or more and therefore
cannot form a corner. So there are three possible ways to construct a regular polyhedra with
triangles. Three and only three squares will form a corner, indicating the possibility of
one regular solid with square faces. The same reasoning yields one possible polyhedron
with three pentagons at each corner. We cannot go beyond the pentagon, because when we
try to put three hexagons together at a corner, they equal 360 degrees. So we have a total
of five regular polyhedra. A slightly more mathematically rigorous proof is at the bottom
of the page.
Are here are the the five platonic solids:
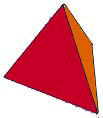
Tetrahedron
4 triangular sides
Cut-out 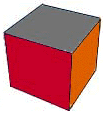
Hexahedron (cube)
6 square sides
Cut-out 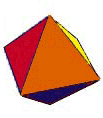
Octahedron
8 triangular sides
Cut-out 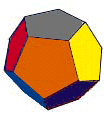
Dodecahedron
12 pentoganal sides
Cut-out 
Icosahedron
20 triangular sides
Cut-out
The slightly-more-rigorous proof:
Euler's formula (for Algebraic Topolgy) states that for a given polyhedron (not neccessarily
regular) the number of Faces minus the number of Edges plus the number of Vertices equals
two, i.e.
F - E + V = 2
Now we look at a regular polyhedron. It has n faces, each one a
k-gon; and at each vertex, p faces are touching. Euler's formula becomes
n - (nk/2) + (nk/p) = 2
We factor this into
n( 1 - (k/2) + (k/p) ) = 2
Since n is positive,
we know that 1 - (k/2) + (k/p) must be greater than zero
(since its product with n is a positive number). Thus we have
1 - (k/2) + (k/p) > 0
We simplify this to
(2/k)+(2/p) > 1
Now for some critical thinking. A k-gon is meaningless when
k = 1 or 2. Additionally, we must have more than two polygons meeting at a
corner, so p > 2
as well.
The only remaining values of k and p that satisfy the equation are
k = 3, p = 3 tetrahedron k = 3, p = 4 octahedron k = 3, p = 5 dodecahedron k = 4, p = 3 cube k = 5, p = 3 isocahedron
Q.E.D.
Return to Mathematrix

4 triangular sides
Cut-out

6 square sides
Cut-out

8 triangular sides
Cut-out

12 pentoganal sides
Cut-out

20 triangular sides
Cut-out