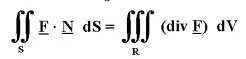Sure, there are lots of topics in mathematics. And for each topic, there is a number of theorems. But only one theorem in each subject area earns the title of
THE FUNDAMENTAL THEOREM OF X
where X is the particular subject in question.
So here we go...
The Fundamental Theorem of Arithmetic:
Any positive integer n can be represented in exactly one way as a product of primes pi:
The Fundamental Theorem of Algebra:
Every Polynomial equation having Complex Coefficients and degree n > 0 has at least one Complex Root.
The five postulates of (Euclidean) Geometry:
(note: we do not list a fundamental theorem here. Rather, we note that all theorems
must follow from a set of statements simply assumed to be true. Since all other theorems
follow from these postulates, we acknowledge said postulates as the "fundamentals".)
1. A straight line segment can be drawn joining any two points.
2. Any straight line segment can be extended indefinitely in a straight Line.
3. Given any straight line segment, a circle can be drawn having the segment as radius
and one endpoint as center.
4. All right angles are congruent.
5. Given a line and a point not on that line, there exists exactly one line through the
given point parallel to the given line. (The parallel postulate)
(note: in Hyperbolic Geometry we replace the parallel postulate by the following:
5. Given a line and a point not on that line, there exist an infinite number of
lines through the given point parallel to the given line.)
(note: in Spherical Geometry (where lines are defined to be great circles on a sphere)
we may replace the parallel postulate by the following:
5. All lines intersect in exactly two points. -- i.e. there are no parallel lines.)
The Fundamental Theorem of Calculus:
If f is a continuous function, then
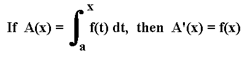
and A'(x) = f(x)
Let f be continuous on [a,b] and let F be an antiderivative for f. Then
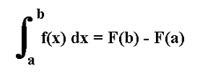
The Fundamental Theorem(s) of Multivariable Calculus:
(Note: technically, all these theorems are a special case of an n-dimensional Stokes' Theorem.)
Green's Theorem: Let C be a simple, closed path, orientated counterclockwise, that encloses Q. Then
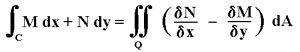
Stokes' Theorem: If the surface S is bounded by the curve C, then
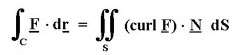
Divergence Theorem (Gauss): If the surface S encloses the region R, then