Fractals

A fractal is a rough or fragmented geometric shape that can be subdivided in parts, each of which is (at least approximately) a reduced-size copy of the whole. This property is call self-similarity. Basically, if you zoom in on one part, its going to look like the bigger picture.

The leaf of a fern is a good example. Fractals also describe many other real-world objects, such as clouds, mountains, turbulence, and coastlines, that do not correspond to simple geometric shapes.

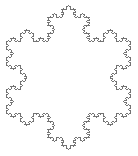
Here is a fractal called the Koch snowflake.
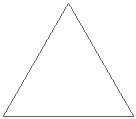
To make it, you start with an equilateral triangle.
Replace each of the lines:
with something that looks like this:
Next, replace each of the lines:
with something that looks like this:
And so on.

Here is what happens to each line:


Here are what the the first few stages of the Koch Snowflake look like:

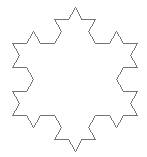
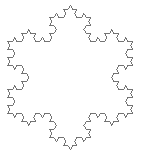
Voila. You have a fractal. Lots of other fractals can be built up in this manner, like the Sierpinski Triangle:

And here's an interesting, somewhat mathematical side note. Imagine you drew a circle the initial triangle used in the Koch snowflake. At no point will the Koch snowflake extend beyond the boundaries of the circle. Thus the snowflake has a finite area (since its area is less than that of the circle, which is finite). However, at every stage in building the snowflake, the perimeter is multiplied by 4/3 - it is always increasing. So the ideal snowflake (ideal meaning you go through an infinite number of stages constructing the figure) has an infinite perimeter (initial perimeter * 4/3 * 4/3 * 4/3 * ...) yet a finite area. Its not a paradox; its simply a fractal.

---

Return to Mathematrix