Important Constants

The significance here should be readily apparent. 1 is the first natural number. 1 is the multiplicative identity (which means multiplying a number by 1 doesn't change the number). And so on.

Zero is a pretty neat number. It means that nothing is there. 0 is the additive identity (which means adding 0 to a number doesn't change the number). 0 is the only number that is not negative or positive. Any number times 0 equals 0. You cannot divide by zero (for instance, let 3/0 = x. Then, 3 = (0)(x). But such a number x does not exist to make this statement true. Therefore, the expression 3/0 is called undefined and we "outlaw" division by zero. But, while you're still reading, consider 0/0 = x. We may rewrite it as 0 = (0)(x), and since this holds for all values of x, we refer to the expression 0/0 as indeterminate. A subtle yet important point.) Also, a⁰ = 1 for all values of a.

An irrational, trascendental number defined as the ratio of a circle's circumference to its diameter.
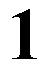
The area of a circle is piradius²
The surface area of a sphere is 4piradius²
The volume of a sphere is (4/3)piradius³
Pi occurs in more than just geometry; for example it has been shown that pi/4 = (1) - (1/3) + (1/5) - (1/7) + (1/9) - (1/11) + ...
And just for fun, here are the first 100 decimal digits of pi:
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679

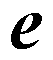
e was named in honor of the great mathematician Euler.
It is interesting that the function f(x) = e^x is its own derivative. Also, we know that
and

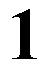
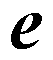
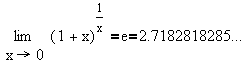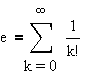Here are the first 100 decimal digits of e:
2.7182818284 5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274
The square root of -1 does not have a solution in the real number system, so we let i represent it. The square roots of negative numbers make up the imaginary numbers. i is to the imaginary numbers what 1 is to the real numbers. Interestingly, we have the formula e^ix= cos(x) + i sin(x). And if we let x = pi, then we have the beautiful result
e^ipi + 1 = 0

This number, phi, is often called the golden ratio, divine proportion, or golden section.

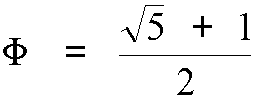
It is the solution to the equation

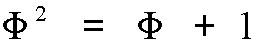
or equivalently,

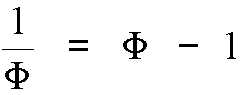
It is said that rectangles whose sides are in this proportion are the most aesthetically pleasing; numerous examples can be found in ancient Greek architecture.
Another geometrical area that it shows up is in a pentagram:

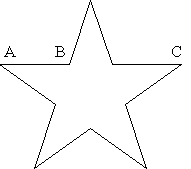
The ratio of AB:BC and AB:AC in a pentagram equals the golden ratio.

In addition, there is a sequence referred to as the Fibonacci sequence, where each term is the sum of the previous two. It begins like this: 0, 1, 1, 2, 3, 5, 8, 13, ...
If we take the ratio of two consecutive terms, this ratio approaches the golden ratio as the terms get larger and larger.
Also, there is an explicit formula for the terms of the Fibonacci sequence, which closely resembles the formula for the golden ratio (as well it should, seeing as how the two are intimately combined):

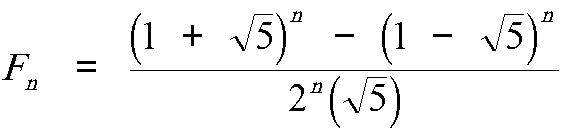
And last but not least, here are the first 100 digits of the golden ratio:
0.6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374

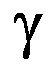
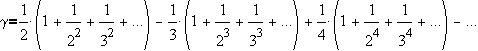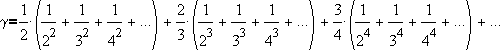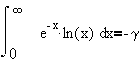Sometimes this is referred to as Euler's constant. It comes up in formulas such as the following:

Return to Mathematrix